ターミナルだけですぐに計算できる
基本は一行のPythonSymPyコードをpythonに渡すだけの仕組み
SymPyとmpmathライブラリの関数を使った一行コードが実行できる
以下仕様のようにもろもろのセッティングが不必要
いちいちpythonを起動、コーディングをしなくても計算できることを追求
【条件】
Bash、zshでの使用OK
python実行環境インストール済み
SymPyライブラリ
mpmathライブラリ
実装環境
macOS12.6.5
Python 3.9.16
Ubuntu22.04.2LTS
Python 3.8.16
【仕様】
入力数式はpython文法
シンボリック変数はaからz
シンボリック関数はf 微分方程式用
sympyとmpmathの関数はすべて使える
分数 2/3 を Frac(2,3)またはFrac(2/3)とすれば分数として計算・出力
おまけ Rumpの例題の検証 入力にrump
【使い方】
ターミナルで
$ pycalc
で本体起動
数値計算式・代数式を入力(変数eq)・rump:
演算精度の桁数(デフォルト1):
ターミナルで
$ pycalcl
で過去入力コードを記録した
$HOME/myscript/pycalcl.txt
を開く
【5通りの出力】
pprint($eq,use_unicode=False)
pprint($eq,use_unicode=True)
pprint(eval('$eq'))
print(eval('$eq'))
pprint(N($eq,${N:- 1}))
【インストール】
HOMEにディレクトリmyscriptをつくる
HOME/myscriptに
pycalc.sh
pycalcl.txt
を配置
MacOSのzshの場合.zshrcに
ubuntuのBashの場合.bashrcに
に以下を追記
source $HOME/myscript/pycalc.sh
一行数式SymPy計算機シェルスクリプト pycalc.sh
# pycalc.sh
function pycalcl(){
open $HOME/myscript/pycalcl.txt
}
function pycalc(){
echo '【One liner SymPy Calculator(一行数式SymPy計算機)】Ver.20230508'
echo ' 商// 剰余% 商と剰余divmod()分数2/3 Frac(2,3) 平方根sqrt(2) 三角関数sin(pi/3) 指数exp() 自然対数log(E**2) 常用対数log(2,10)'
echo ' 虚数j(標準) (2+3j)*(5-7j)'
echo ' 虚数I(SymPy) exp(cos(E**I)+sin(E*pi)) I**I'
echo ' 素因数分解 factorint(1000) 階乗factorial(10)'
echo ' 代数演算 シンボリック変数aからz expand((x+y)**10) factor(a**10-b**10) '
echo ' 数列 Sum(k**2,(k,1,n)).doit()'
echo ' 方程式 solve(a*x**2+b*x+c,x) 連立方程式 solve([x+y-4,x-y-2],[x,y])'
echo ' 微分方程式 変数はf限定 dsolve(Eq(f(t).diff(t, t) - f(t), exp(t)), f(t))'
echo ' 微分 diff(x**2,x) 積分integrate(x**3,x) 定積分integrate(x**3,(x,0,1))'
echo ' 無限oo integrate(1/(1+x**2), (x, -oo, oo)) '
echo ' テイラー展開 series(sin(x),x, 0, 12)'
echo ' テイラー展開 係数リスト taylor(sin, 0, 5)'
echo ' 行列 Matrix([[1, 2], [2, 2]]).eigenvals()'
echo ' 関・ベルヌーイ数 bernoulli()'
echo ' ゼータ zeta() zetazero()'
echo ' ブール値検算 1+1 == 3 expand((x+y)**2) == x**2 + 2*x*y + y**2'
echo ' グラフ plot(x**2, (x, -1, 2), ylabel = "y")'
echo ' mpmath任意精度浮動小数点演算パッケージによる精度計算 (-2)**mpf("0.5")'
echo ' Rumpの例題 入力にrump https://ja.wikipedia.org/wiki/%E7%B2%BE%E5%BA%A6%E4%BF%9D%E8%A8%BC%E4%BB%98%E3%81%8D%E6%95%B0%E5%80%A4%E8%A8%88%E7%AE%97'
echo -e '\n数値計算式・代数式(変数eq)・rump:'
read eq
echo -n '\n演算精度の桁数(デフォルト1):'
read N
echo "$eq" >> $HOME/myscript/pycalcl.txt
echo -E "
from mpmath import *
mp.pretty = True
from sympy import *
from fractions import Fraction as Frac
init_printing()
var('a:z')
f = Function('f')
rump = 'rump'
if $eq == 'rump':
a=77617
b=33096
c=333.75*b**6+a**2*(11*a**2*b**2-b**6-121*b**4-2)+5.5*b**8+a/(2*b)
print(f'通常計算{c}')
def g(a, b):
return (mpf('333.75')*b**6 + a**2*(11*a**2*b**2-b**6-121*b**4-2)+mpf('5.5')*b**8+a/(mpf('2')*b))
for mp.dps in range(1, $N+1):
print(mp.dps,g(mpf('77617'), mpf('33096')))
else:
mp.dps = ${N:- 1}
# mp.prec = 200
print('\npprint($eq,use_unicode=False)')
pprint($eq,use_unicode=False)
print('\npprint($eq,use_unicode=True)')
pprint($eq,use_unicode=True)
print('\npprint(eval(eq))')
pprint(eval('$eq'))
print('\nprint(eval(eq))')
print(eval('$eq'))
print('\nN($eq,${N:- 1})')
pprint(N($eq,${N:- 1}))
" | python
}
使用例
初等関数・分数
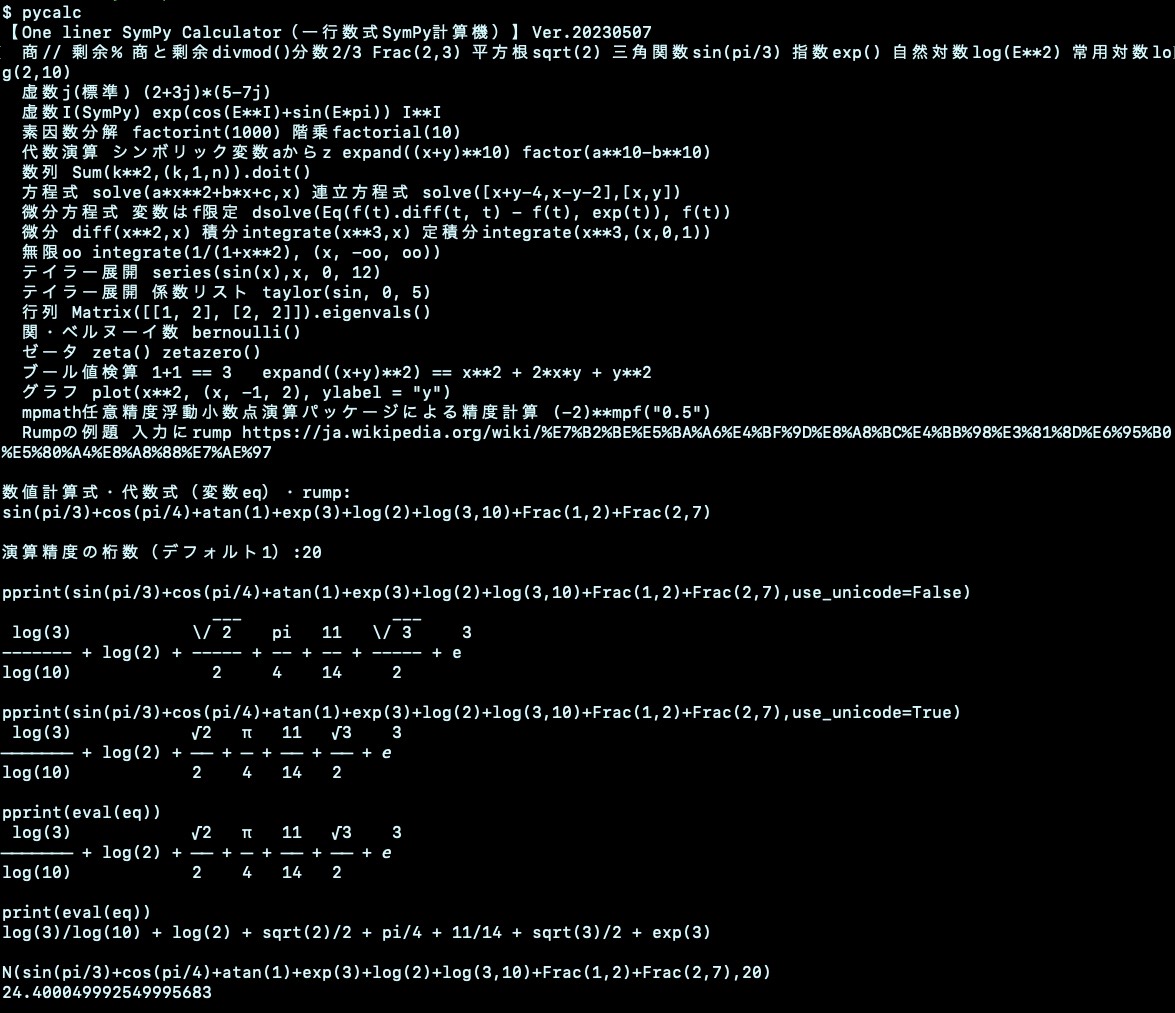
虚数
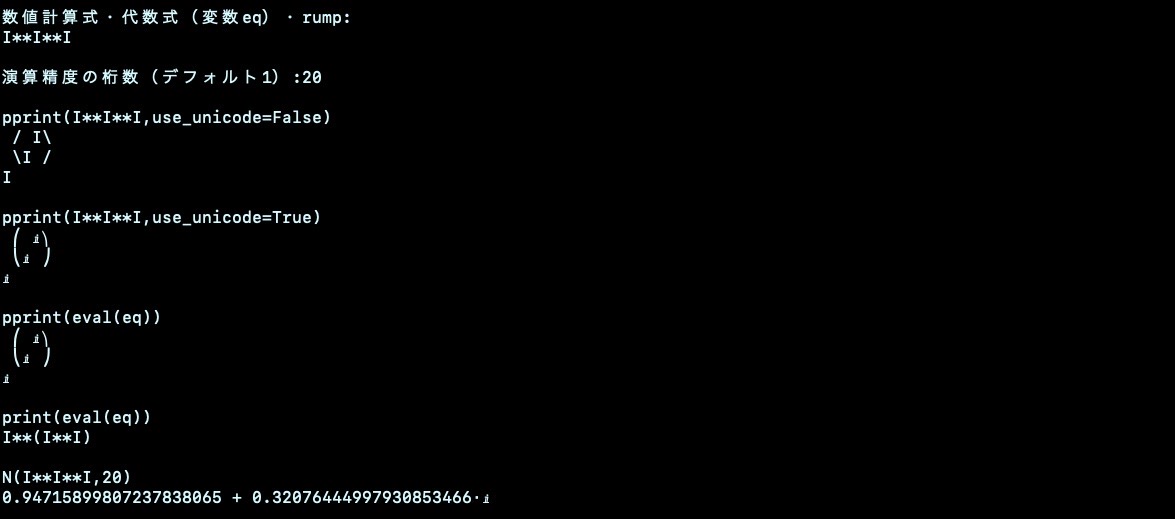
分数
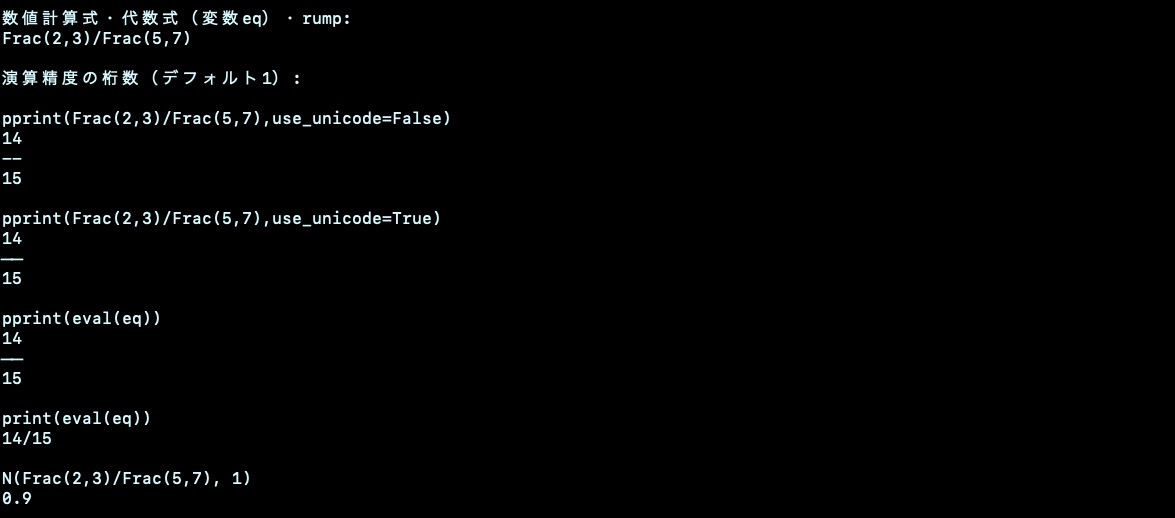
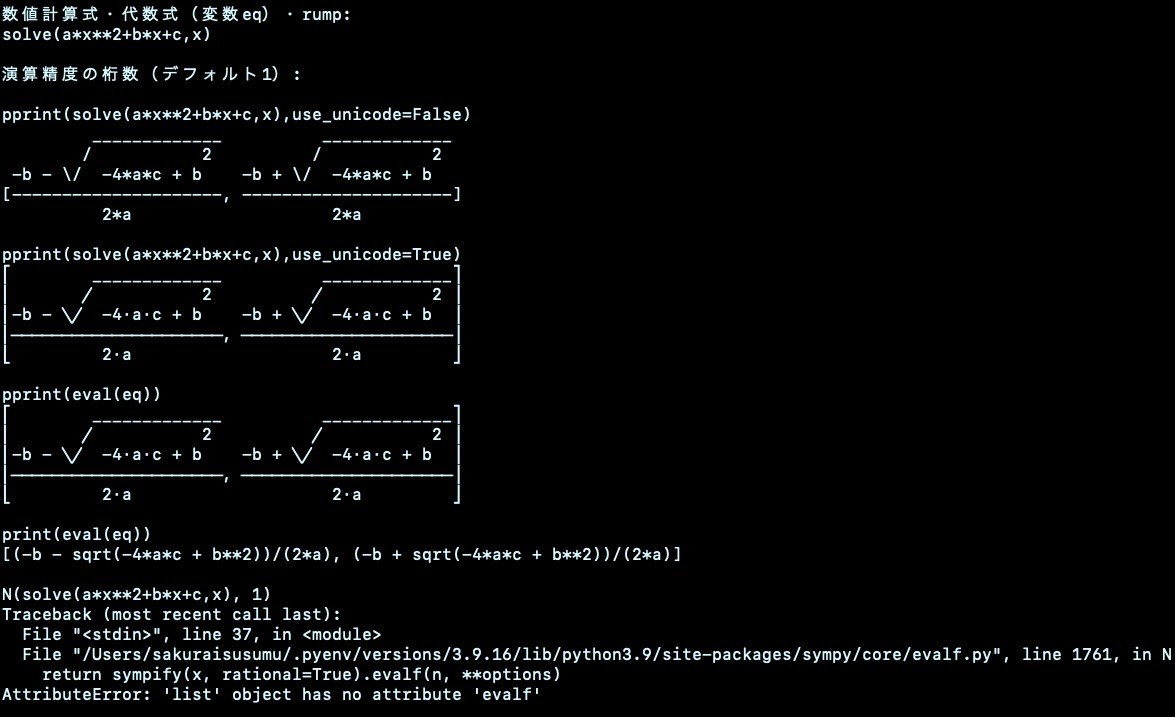
方程式
逆行列
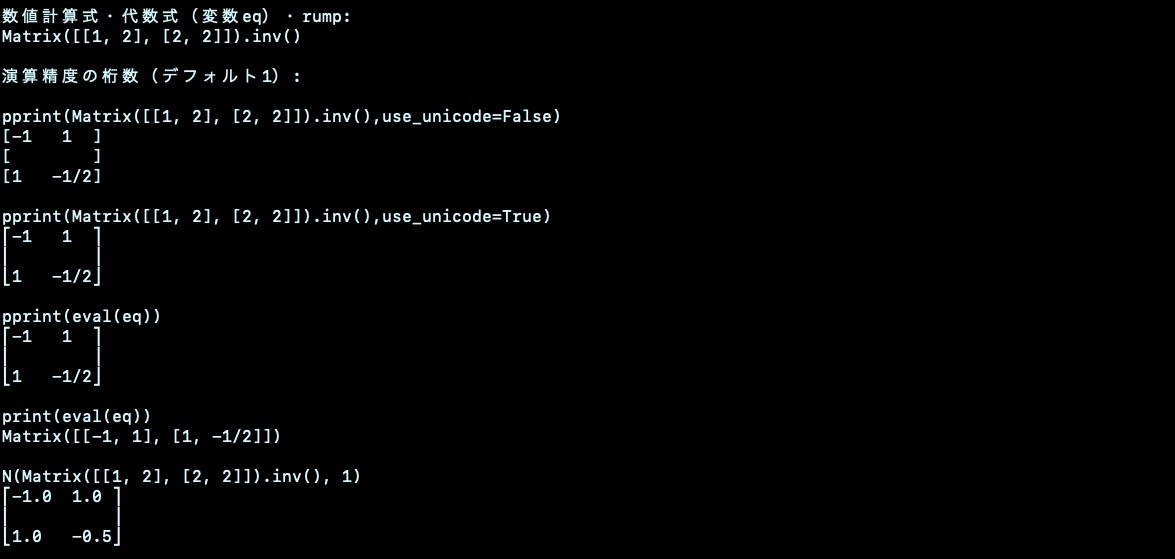
微分方程式
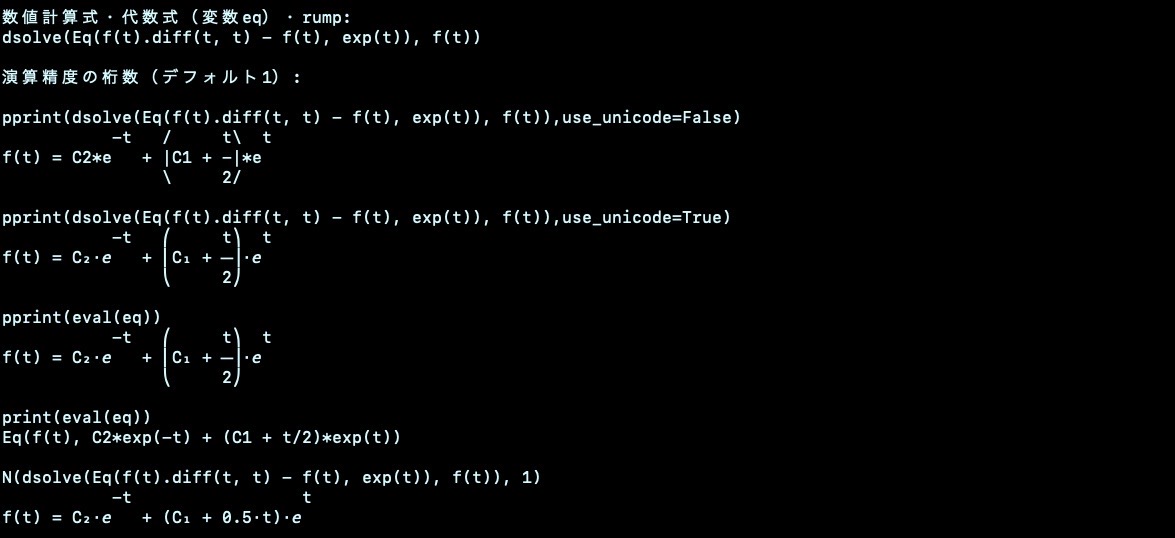
検算
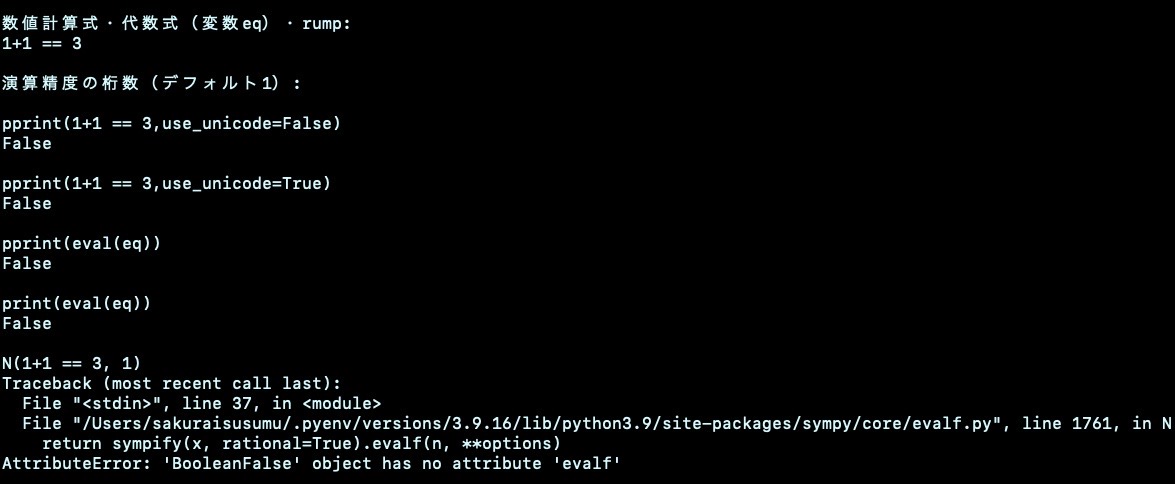
検算
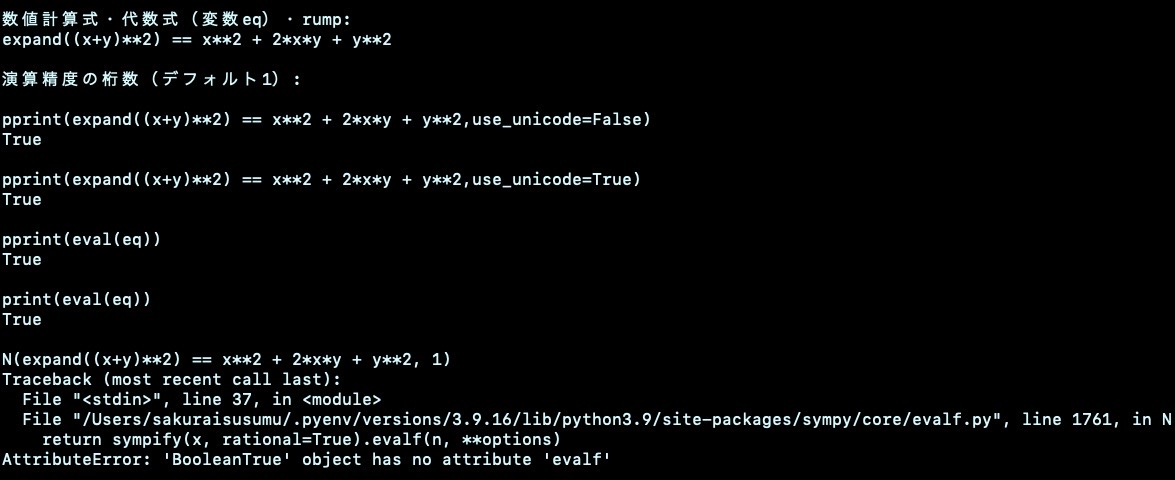
任意精度浮動小数点演算
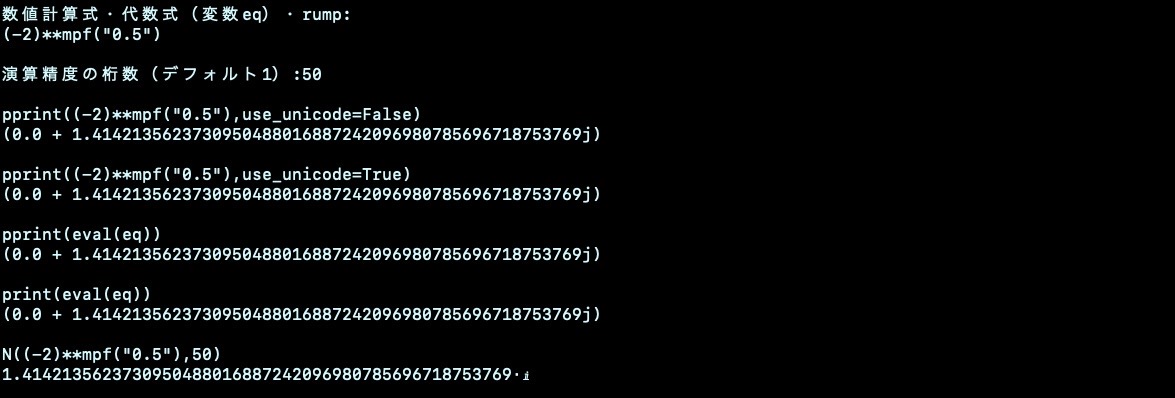
Rumpの例題の検証

