2021年12月 – ssf

■12月12日(日)11:00-12:00 桜井進のPython･UNIX・Math教室（応用コース）

超入門・Pythonで関・ベルヌーイ数

My code
Akiyama-Tanigawa algorithm
B(n) is just sum of k^n formula linear term coefficient.
Zeta function algorithm

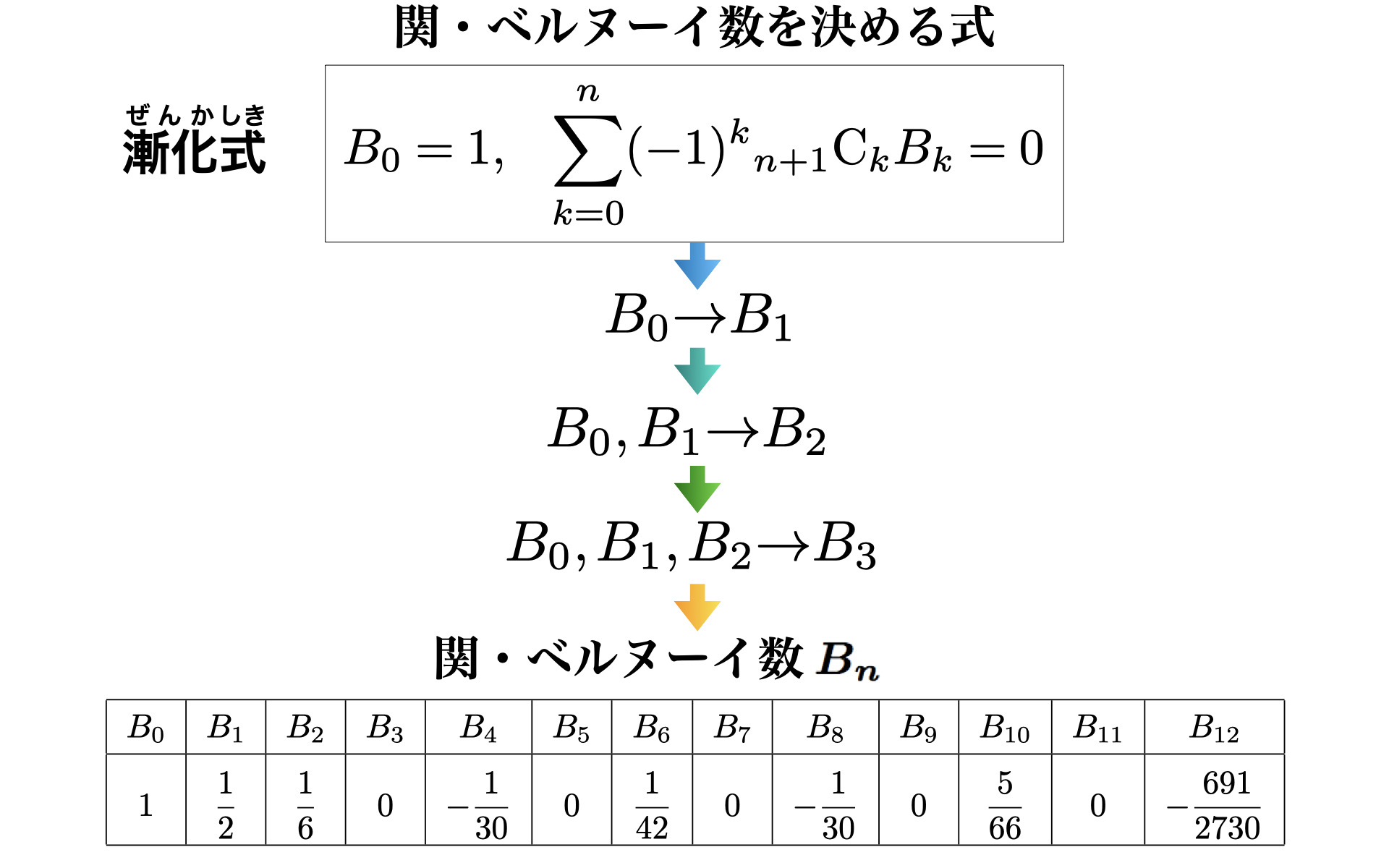
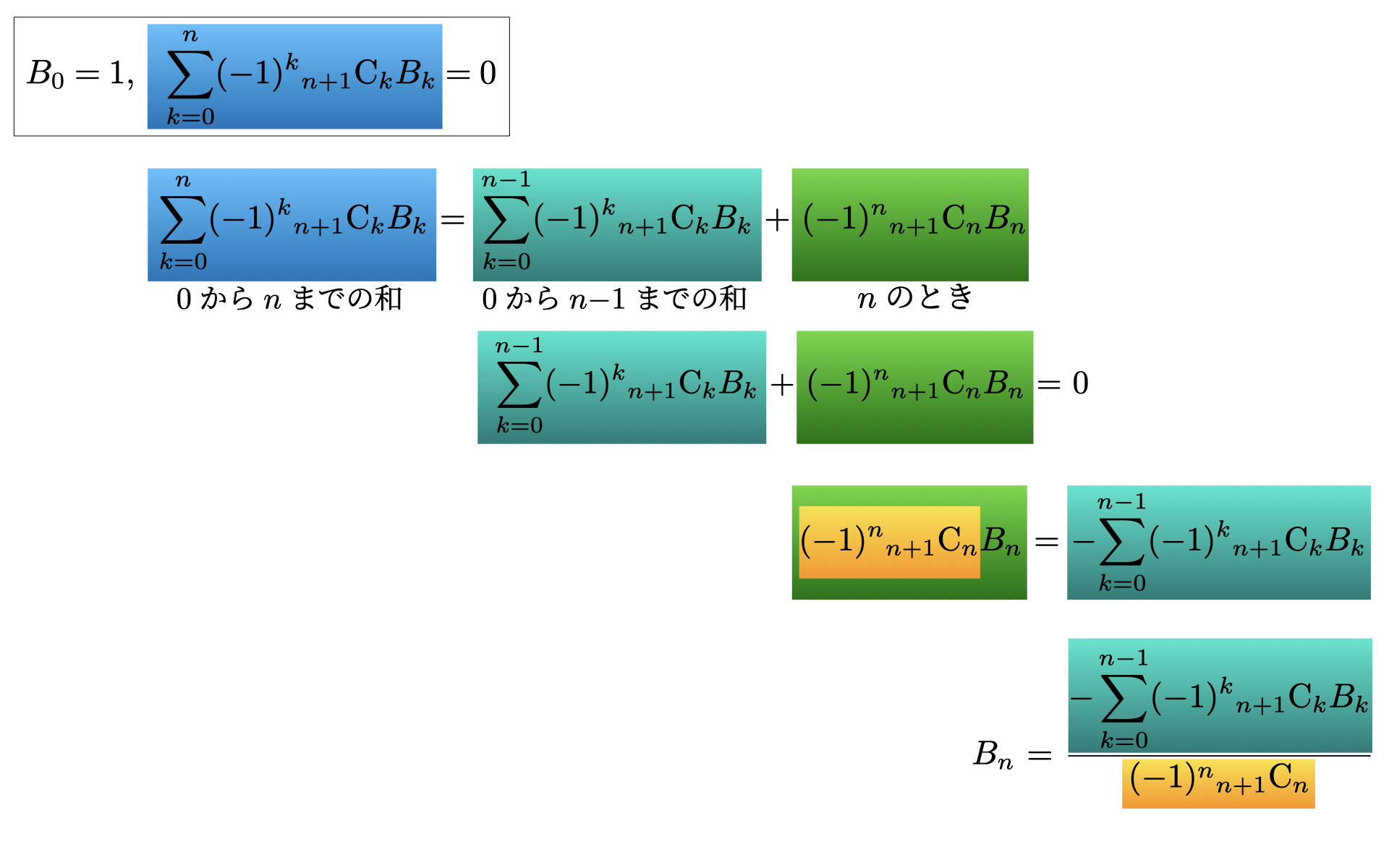
# 1. My code
# seki-bernoulli_1.py

from fractions import Fraction

# 二項係数 Combination nCk
def comb(n, k):
    prod = 1
    for t in range(min(k, n-k)):
        prod = prod * (n-t)//(t+1)
    return prod

# Seki-Bernoulli number Bn
def B(n):
    if n == 0:
        return 1
    else:
        ss = 0
        for k in range(0, n):
            ss = ss + ((-1)**k) * comb(n+1, k)*B(k)
        return Fraction((-1)**(n+1), n+1) * ss


n = int(input('B(n)のnの上限 >>> '))
import sympy
for i in range(n + 1):
    print(f"B({i})= {B(i)}".ljust(20, " "),f"sympy.bernoulli({i})=",sympy.bernoulli(i))

実行結果

$ python seki-bernoulli_1.py
B(n)のnの上限 >>> 20
B(0)= 1              sympy.bernoulli(0)= 1
B(1)= 1/2            sympy.bernoulli(1)= -1/2
B(2)= 1/6            sympy.bernoulli(2)= 1/6
B(3)= 0              sympy.bernoulli(3)= 0
B(4)= -1/30          sympy.bernoulli(4)= -1/30
B(5)= 0              sympy.bernoulli(5)= 0
B(6)= 1/42           sympy.bernoulli(6)= 1/42
B(7)= 0              sympy.bernoulli(7)= 0
B(8)= -1/30          sympy.bernoulli(8)= -1/30
B(9)= 0              sympy.bernoulli(9)= 0
B(10)= 5/66          sympy.bernoulli(10)= 5/66
B(11)= 0             sympy.bernoulli(11)= 0
B(12)= -691/2730     sympy.bernoulli(12)= -691/2730
B(13)= 0             sympy.bernoulli(13)= 0
B(14)= 7/6           sympy.bernoulli(14)= 7/6
B(15)= 0             sympy.bernoulli(15)= 0
B(16)= -3617/510     sympy.bernoulli(16)= -3617/510
B(17)= 0             sympy.bernoulli(17)= 0
B(18)= 43867/798     sympy.bernoulli(18)= 43867/798
B(19)= 0             sympy.bernoulli(19)= 0
B(20)= -174611/330   sympy.bernoulli(20)= -174611/330

案の定、関数B(n)は再帰的定義をしているため、B(30)の計算はできません。
結果をsympy.bernoulli()と比較してみます。

このアルゴリズムはヤコブ・ベルヌーイによるべき乗和による導入によるもの
したがって、$B(1)=\frac{1}{2}$
sympy.bernoulli(1)=-1/2 は、現在主流である母関数$\frac{x}{e^x-1}$による関・ベルヌーイ数の定義

次はゼータの負の整数に対する公式によるもの
関数mpmath.zeta()を用いるだけのコード

# 4 zeta fuction algorithm
# seki-bernoulli_4.py

print('4 zeta fuction algorithm')
n = int(input('B(n)のnの上限 >>> '))

from mpmath import zeta
def B(m):
    b = -m * zeta(1-m)
    return b

from sympy import *
for i in range(1, n + 1):
    b = B(i)
    c = Rational(b)
    print(f"B({i})= {c}".ljust(20, " "),f"sympy.bernoulli({i})=",bernoulli(i))

実行結果

$ python seki-bernoulli_4.py
4 zeta fuction algorithm
B(n)のnの上限 >>> 50
B(1)= 1/2            sympy.bernoulli(1)= -1/2
B(2)= 1/6            sympy.bernoulli(2)= 1/6
B(3)= 0              sympy.bernoulli(3)= 0
B(4)= -1/30          sympy.bernoulli(4)= -1/30
B(5)= 0              sympy.bernoulli(5)= 0
B(6)= 1/42           sympy.bernoulli(6)= 1/42
B(7)= 0              sympy.bernoulli(7)= 0
B(8)= -1/30          sympy.bernoulli(8)= -1/30
B(9)= 0              sympy.bernoulli(9)= 0
B(10)= 5/66          sympy.bernoulli(10)= 5/66
B(11)= 0             sympy.bernoulli(11)= 0
B(12)= -691/2730     sympy.bernoulli(12)= -691/2730
B(13)= 0             sympy.bernoulli(13)= 0
B(14)= 7/6           sympy.bernoulli(14)= 7/6
B(15)= 0             sympy.bernoulli(15)= 0
B(16)= -3617/510     sympy.bernoulli(16)= -3617/510
B(17)= 0             sympy.bernoulli(17)= 0
B(18)= 43867/798     sympy.bernoulli(18)= 43867/798
B(19)= 0             sympy.bernoulli(19)= 0
B(20)= -174611/330   sympy.bernoulli(20)= -174611/330
B(21)= 0             sympy.bernoulli(21)= 0
B(22)= 854513/138    sympy.bernoulli(22)= 854513/138
B(23)= 0             sympy.bernoulli(23)= 0
B(24)= -236364091/2730 sympy.bernoulli(24)= -236364091/2730
B(25)= 0             sympy.bernoulli(25)= 0
B(26)= 8553103/6     sympy.bernoulli(26)= 8553103/6
B(27)= 0             sympy.bernoulli(27)= 0
B(28)= -23749461029/870 sympy.bernoulli(28)= -23749461029/870
B(29)= 0             sympy.bernoulli(29)= 0
B(30)= 8615841276005/14322 sympy.bernoulli(30)= 8615841276005/14322
B(31)= 0             sympy.bernoulli(31)= 0
B(32)= -7709321041217/510 sympy.bernoulli(32)= -7709321041217/510
B(33)= 0             sympy.bernoulli(33)= 0
B(34)= 2577687858367/6 sympy.bernoulli(34)= 2577687858367/6
B(35)= 0             sympy.bernoulli(35)= 0
B(36)= -26315271553053477373/1919190 sympy.bernoulli(36)= -26315271553053477373/1919190
B(37)= 0             sympy.bernoulli(37)= 0
B(38)= 2929993913841559/6 sympy.bernoulli(38)= 2929993913841559/6
B(39)= 0             sympy.bernoulli(39)= 0
B(40)= -261082718496449122051/13530 sympy.bernoulli(40)= -261082718496449122051/13530
B(41)= 0             sympy.bernoulli(41)= 0
B(42)= 1520097643918070802691/1806 sympy.bernoulli(42)= 1520097643918070802691/1806
B(43)= 0             sympy.bernoulli(43)= 0
B(44)= -27833269579301024235023/690 sympy.bernoulli(44)= -27833269579301024235023/690
B(45)= 0             sympy.bernoulli(45)= 0
B(46)= 596451111593912163277961/282 sympy.bernoulli(46)= 596451111593912163277961/282
B(47)= 0             sympy.bernoulli(47)= 0
B(48)= -5609403368997817686249127547/46410 sympy.bernoulli(48)= -5609403368997817686249127547/46410
B(49)= 0             sympy.bernoulli(49)= 0
B(50)= 495057205241079648212477525/66 sympy.bernoulli(50)= 495057205241079648212477525/66

月: 2021年12月

関・ベルヌーイ数　Pythonコード

超入門・Pythonで関・ベルヌーイ数