12月26日(日)14:30-16:30桜井進の数学浪漫紀行

小数点「.」誕生402年記念
驚異の数円周率π 2021
人はなぜπを計算しつづけるのか

2000年、サイエンスナビゲーターⓇに変身してから毎年アップデートした
πの物語を語りつづけてきました
2021年も万感をこめてサイエンスナビゲーターⓇはπを語ります

申込Peatix
http://ptix.at/G3xXUI

12月12日（日）11:00-12:00 桜井進のPython･UNIX・Math教室（応用コース）

超入門・Pythonで
関・ベルヌーイ数

1712年関孝和
1713年ヤコブ・ベルヌーイ
に発表された関・ベルヌーイ数Bn

300年経った現在でも現在進行形
その一つが
算出アルゴリズムの発見
関・ベルヌーイ数算出Pythonコードをいくつも紹介します
・桜井進のコード
・Akiyama–Tanigawa algorithm
・B(n) is just sum of k^n formula linear term coefficient.
・Zeta function algorithm

1時間の授業で一気に総覧できるのも
電子計算機とPythonのおかげ

申込Peatix
http://ptix.at/KsZh4I

小学生からわかる
超入門
関・ベルヌーイ数

自然数のたし算に現れる関・ベルヌーイ数
300年前に日本人数学者関孝和によって発見
同時期にヤコブ・ベルヌーイによっても発見

関・ベルヌーイ数はフィボナッチ数と同じく数列
関・ベルヌーイ数を知る1時間
関・ベルヌーイ数を一度知ったら興味がどんどんわいてくることでしょう

■申込
Peatix 桜井進の算数・数学教室
（クレジットカード・コンビニATM・PayPal）
https://sakuraiclass.peatix.com/

9・10月共通テーマ「超入門・ゼータ関数」
10月17日（日）11:00-12:00 桜井進のPython･UNIX・Math教室（応用コース）

Pythonでゼータを操る
mpmath.zeta(-1)とゼータ関数のオイラー積
1億個の素数をつかってゼータのオイラー積の精度を検証

1億個の素数リスト生成に成功

このファイルがあれば素数を使った数値実験がさまざまできます

第1弾はゼータのオイラー積の数値計算
私が知るかぎりオイラーもこの計算は行っていません

私も計算してみるまでは計算精度はわかりませんでした
想像してみてください
２、３、５、とつづく素数を1億個を使ったかけ算がいくつになるのか
結果は授業で公開します
お楽しみに

■受講条件
Python実行環境がインストールされたPCがあること

■Peatix
http://ptix.at/3wkFOE

超入門・ゼータ関数　オイラー、計算の旅

参加者　13名（小学生1名、高校生1名、大人11名）
テキストPDF 26ページ

関・ベルヌーイ数の漸化式

オイラーの計算の旅を2時間で駆け巡りました

■次回　10月24日(日)14:30-16:30桜井進の数学浪漫紀行

超入門・ゼータ関数
オイラーゼータからリーマンゼータへ

Peatix
http://ptix.at/4g65Nc

小学生からわかる 超入門・ゼータ関数

参加者 6組親子（6歳、小学生3名、中学生1名、高校生1名）
テキストPDF 21ページ

長年の構想がついに実現！
小学生からわかる
超入門・ゼータ関数

オイラーの無限のたし算を鑑賞
先取り学習でも受験勉強でもありません
そもそも勉強ではありません
もはや勉強ばかりしている時代は終わった

６歳と小学生たちを人としてあつかう
子供扱いをしない
これがサイエンスナビゲーターⓇのモットー

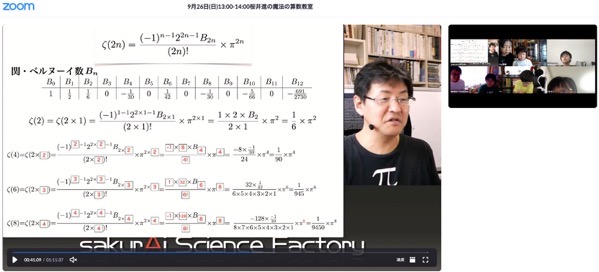
人に与えられたインテリジェンス
知的好奇心に
私は語りかけます
Mathematicsの感動を

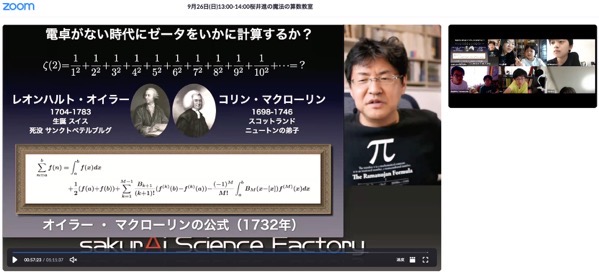
オイラーの計算はまさにマジック
でもこれがマジックに終わらないのが
Mathematicsの驚異

リーマン
ラマヌジャン
グロダンディーク
といった化け物・妖怪たちのインテリジェンスを駆り立て
20世紀のMathematicsがつくられていった
やはりオイラーのマジックだ

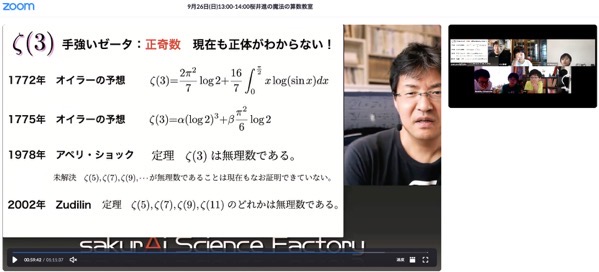
ゼータはわからないことばかり
つぎに解き明かすのは君たちだ

ゼータの計算のたびははじまって300年足らず
長い旅がこれからもつづく

ワクワクした
面白かった
もっと知りたい
という参加者の皆様の感想
エキサイティングな60分はあっという間に終わりました

■次回は今回のつづき

10月24日(日)13:00-14:00桜井進の魔法の算数教室
小学生からわかる
超入門・ゼータ関数
素数が無限にあることの証明

Peatix
http://ptix.at/EK45t4

桜井進の算数・数学教室9月・10月共通テーマ
超入門・ゼータ関数

超入門・ゼータ関数

オイラー、計算の旅

18世紀、少年オイラーがスイスのバーゼルで知った問題
自然数の2乗の逆数の無限和はいくつになるか
10年に渡る計算の旅の末にたどり着いた終着駅

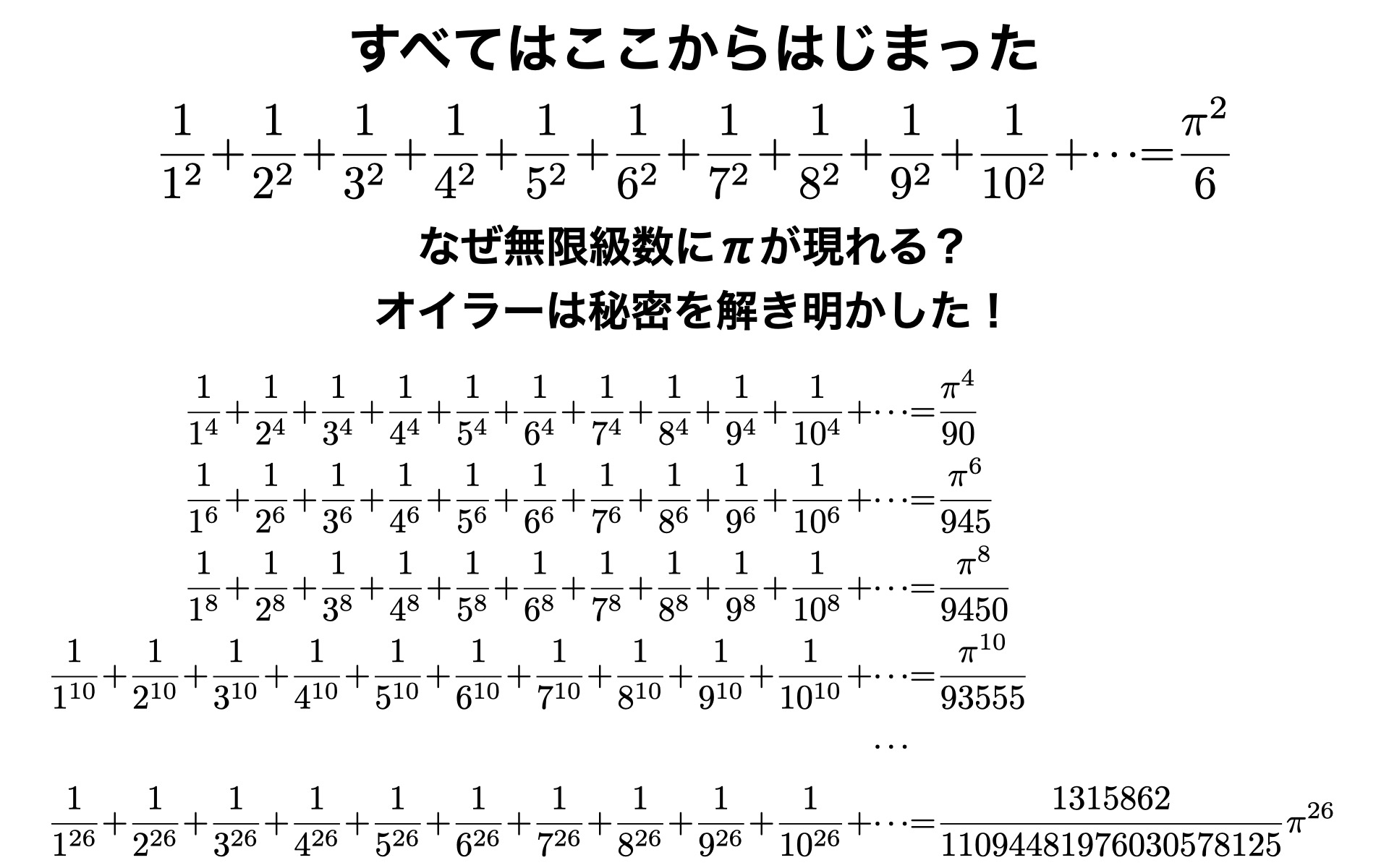
驚くべきことに円周率πが出迎えてくれた
なぜπが現れるのか
オイラーの挑戦はつづいた
証明の鍵は、三角関数、微分積分、そして対数
1735年、28歳のオイラーはその全貌を解き明かした

そして手にいれたのがゼータ関数

オイラーはここを始発駅として
あらたな計算の旅に出る
さらに驚きの風景がオイラーを待っていた

まさに数学はマジック！
無限にたし算できるマジック
数の世界のルールこそマジックのタネ明かし
数の世界に秘められた驚異のルールをオイラーの超絶技巧が解き明かす

数式美術館巡りをしましょう
たし算の驚きの風景に遭遇します

■Peatix
http://ptix.at/nj72nU

小学生からわかる
超入門・ゼータ関数

無限にたし算を考えたオイラー
250年前にオイラーが描いてみせた不思議なたし算
数式美術館巡りをしてみましょう
驚異のたし算の風景画にびっくり

■対象
小学１年生以上、親子で参加（大人は1人でもOK）

■Peatix
http://ptix.at/6gq2me

■9/26(日)13:00-14:00 桜井進の魔法の算数教室　【小学生からわかる　超入門・ゼータ関数　オイラーの無限のたし算を鑑賞】
■9/26(日)14:30-16:30 桜井進の数学浪漫紀行　【超入門・ゼータ関数　オイラー、計算の旅】

■10/17(日)11:00-12:00 桜井進のPython・UNIX・Math教室　【Pythonでゼータを操る】
■10/24(日)13:00-14:00 桜井進の魔法の算数教室　【小学生からわかる　超入門・ゼータ関数　素数が無限にあることの証明】
■10/24(日)14:30-16:30 桜井進の数学浪漫紀行　【超入門・ゼータ関数　オイラーゼータからリーマンゼータへ】

■申込
桜井進の算数・数学教室の申込はPeatixに統一しました
□Peatix 桜井進の算数・数学教室
（クレジットカード・コンビニATM・PayPal）
https://sakuraiclass.peatix.com/

バーゼルの問題

オイラー、計算の旅

参加者　大人11名 子供1名

1. 調和級数 自然数の逆数の無限和
2. バーゼルの問題 自然数の2乗逆数の無限和
3. オイラーの挑戦
4. オイラーの成功
5. ゼータの発見

18世紀、少年オイラーがスイスのバーゼルで知った問題
自然数の2乗の逆数の無限和はいくつになるか
10年に渡る計算の旅の末にたどり着いた終着駅

\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^3}+\frac{1}{4^2}\cdots = \frac{\pi^2}{6}

驚くべきことに円周率πが出迎えてくれた
なぜπが現れるのか
オイラーの挑戦はつづいた
証明の鍵は、三角関数、微分積分、そして対数
1735年、28歳のオイラーはその全貌を解き明かした

オイラーはここを始発駅として
あらたな計算の旅に出る
さらに驚きの風景がオイラーを待っていた

1+2+3+4+5+6+7+8+9+10+11+\cdots =-\frac{1}{12}

まさに数学はマジック！
無限にたし算できるマジック
数の世界のルールこそマジックのタネ明かし
数の世界に秘められた驚異のルールをオイラーの超絶技巧が解き明かす